Mandelbrot set

I have created fast some coloring method to show it can look very different.

References

Mandelbrot-halmaz a Wikipédián

Bertalan Ágnes - A Mandelbrot halmaz - 2011

Bastian Fredriksson - An introduction to the Mandelbrot set - January 2015

Julia set at Wikipedia

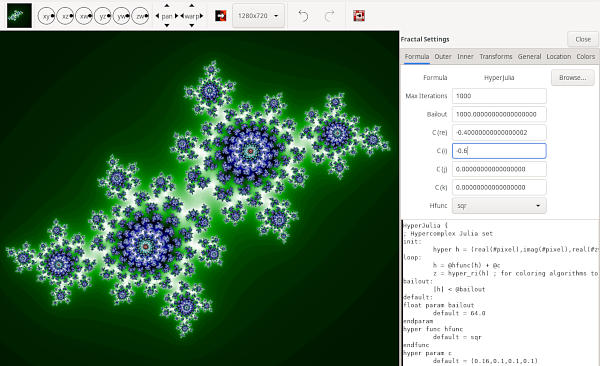
GnoFract 4D

If you would like to extract fractal images under Linux you can try GnoFract 4d.

Mathworks - MATLAB

Available for Linux. - https://www.mathworks.com/

"MATLAB is a programming and numeric computing platform used by millions of engineers and scientists to analyze data, develop algorithms, and create models."

GNU Octave

GNU Octave website: Powerful mathematics-oriented scientific programming language with 2D/3D plotting and Matlab script compatibility

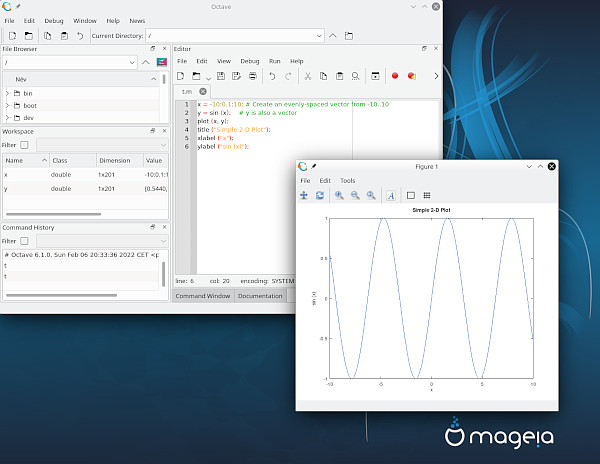
My simple code for Mandelbrot set in GNU Octave:

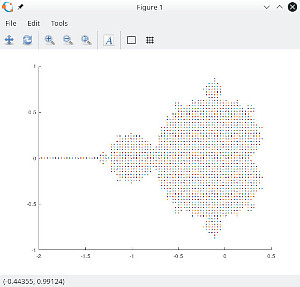
itercount = 1000;
bailout = 10;
step = 0.03 #decrease step for better resolution

x=-2;
y=-1.2;
hold ("on");
for x = -2:step:1
  for y=-1.2:step:1.2
      n=0;
      absz = 0;
      a = 0;      #complex z = (a,b)
      b = 0;
      do
        newx = a*a - b*b + x; #real of z^2+c
        newy = 2*a*b + y;     #imag of z^2+c
        a = newx;             #z(n+1) = (newx, newy)
        b = newy;
        absz = sqrt(a*a + b*b);  #abs(z)
        n++;
      until ((n==itercount) || (absz>bailout))
      if (n==itercount) 
         plot( x , y ) ;
      endif
   endfor
endfor
hold ("off");

Happily Octave knows arithmetical operations on complex numbers, so you can make easier script.

Mandelbrot_iter.m

#
# Returns the number of succesfull iterations
#
function retval = Mandelbrotxy( z, e, c, maxiter, bailout )
  n = 0;
  do
     z =  z.^e + c;
     n++;
  until ( (abs(z)>bailout) || (n==maxiter) );
  retval = n;
endfunction

Mandelbrot_set.m

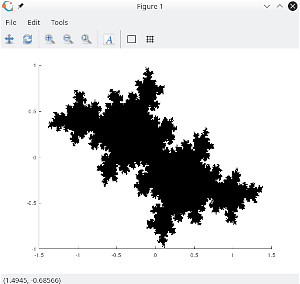
texts = {"Max iteration", "Bailout", "Step","Exponent of z^n+c","cx","cy"};
defaultvalues = {"1000", "10", "0.05","2","0","0"};
inputsizes = [1,10; 1,10; 1,10; 1,10; 1,10; 1,10];
settings = inputdlg (texts, "Settings", inputsizes, defaultvalues); 

maxiter = str2num(settings{1});
bailout = str2num(settings{2});
step = str2num(settings{3});
exponent = str2num(settings{4});
cx = str2num(settings{5});
cy = str2num(settings{6});
if (maxiter<=0)
  maxiter = 1000;
endif
if (bailout<=0)
  bailout = 10;
endif
if (step<=0) || (step>=1)
  step = 0.05;
endif
if (exponent<1) || (exponent>=50  )
  exponent = 2;
endif

hold('on');
for x= -2:step:2;
  for y= -1.2:step:1.2;
    if ((cx==0) && (cy==0)) # Mandelbrot
      z0 = 0;               #  z0 = 0;
      c = complex(x,y);     # (x,y) for Mandelbrot
    else                    # Julia
      z0 = complex(x,y);    # z0 = (x,y) for Julia      
      c = complex(cx,cy);   # e.g. -0.442444, 0.556128
    endif
    n = Mandelbrot_iter( z0, exponent,  c, maxiter, bailout )
    if (n==maxiter)
      plot( x, y );
    endif
  endfor
endfor
hold('off');

Plotting to figure is the simplest way for displaying set, more colorfull solution is creating an image and assigning a color from colormap to iteration number. My favourite to create Z with a meshgrid and generate the iteration number matrix at once using filter mask, and the result array can be displayed with imagesc. In this case you can work with result data further more before displaying and also you can save/export for later use and then just have to importdata.

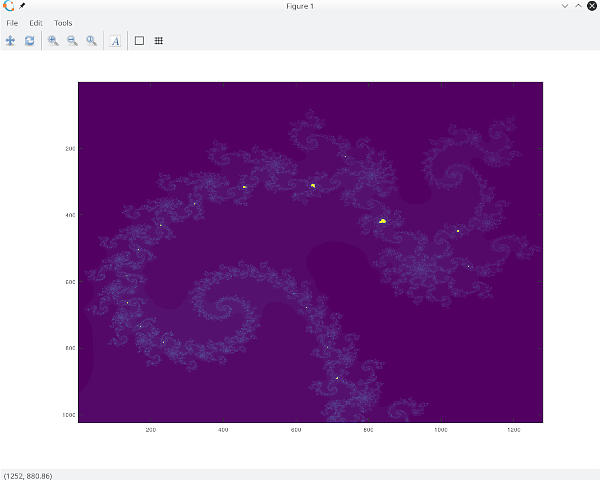
π as Dave Boll discovered:

Calc_PI_with_Mandelbrot.m with (−0.75, ε)

#
# Calculate PI with Mandelbrot  /discovered by Dave Boll/
#

n = 6; #number of decimals

z0 = 0;                # z0 = complex( 0,0 );
exponent = 2;
cx = -0.75;            # by Dave Boll
cy = 1/10^n;
c = complex( cx, cy );
bailout = 2;
calcpi =  Mandelbrot_iter( z0, exponent, c, 0, bailout );
printf("PI = 3,1415926535 ... /n");
printf("Calculated Pi~: %f /n",calcpi*cy);

Another route with (0.25+ε ,0)

z0 = 0;
exponent = 2;

for n = 0:1:11;
  e = 1/10^n;
  cx = 0.25+e;
  cy = 0;
  c = complex( cx, cy );
  bailout = 2;

  calcpi =  Mandelbrot_iter( z0, exponent, c, 0, bailout );
  printf("Calculated Pi~: %f /n",calcpi*sqrt(e));
endfor

printf("PI = 3,1415926535 ... /n");

Refferences:

https://www.cheenta.com/pi-calculating-from-mandelbrot-set-using-julia/

https://www.doc.ic.ac.uk/~jb/teaching/jmc/pi-in-mandelbrot.pdf

GNU bc

"bc is an arbitrary precision numeric processing language." https://www.gnu.org/software/bc/bc.html

Menu

1. Tóthpál István - Home

2. Weblinks

3. Curriculum Vitae

4. Photography

5. Trips

   • Hungary

   • Austria

   • Croatia

   • Czech Republic

   • Greece

   • Poland

   • Slovakia

6. Fishing

7. Linux

   • 3DObjectsCAD

   • Cryptomining

   • Games

   • Android Development

   • Audio, Music

   • Mandelbrot set

   • Photo Editing

   • WebGL

   • OpenGL

8. HW Programming